D2
Администратор
- Регистрация
- 19 Фев 2025
- Сообщения
- 4,380
- Реакции
- 0
Автор: shqnx
Специально для ~/XSS.IS
Эллиптическая кривая представляет собой геометрическую структуру, определяемую уравнением вида:
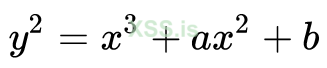
(★),где a и b - параметры, определяющие форму и расположение кривой, а x и y - координаты точки на кривой. Важно отметить, что эллиптические кривые определены над полем, которое обычно является полем вещественных чисел или конечным полем.
- Уравнение кривой: Уравнение (★) определяет форму эллиптической кривой. Коэффициенты a и b влияют на ее кривизну и форму.
- Операции над точками: Операции над точками на эллиптической кривой включают в себя сложение точек и удвоение точек. Сложение точек определяется геометрически и связано с поиском пересечения кривой с прямой, проходящей через две заданные точки. Удвоение точки также является геометрической операцией, представляющей собой поиск касательной к кривой в заданной точке и нахождение её второго пересечения с кривой.
Эллиптические кривые нашли широкое применение в криптографии благодаря своим уникальным математическим свойствам, которые делают их особенно подходящими для различных криптографических задач. Основные преимущества использования эллиптических кривых включают в себя:
- Безопасность: Эллиптические кривые обеспечивают высокий уровень безопасности при использовании в криптографических протоколах. Это связано с тем, что проблема дискретного логарифмирования на эллиптических кривых сложнее для решения по сравнению с аналогичными задачами для других математических структур.
- Эффективность: В сравнении с классическими методами криптографии, такими как RSA, использование эллиптических кривых позволяет достигать того же уровня безопасности при меньших объемах ключей и операций.
- Масштабируемость: Эллиптические кривые позволяют строить криптографические протоколы, способные работать с небольшими вычислительными ресурсами.
Группой точек на эллиптической кривой называется множество всех точек кривой вместе с определенной операцией, обычно называемой сложением точек. Формально, пусть E - эллиптическая кривая, а P и Q - две её точки. Операция сложения P+Q определяется геометрически и зависит от конкретного вида кривой. Основные свойства группы точек на эллиптической кривой включают:
- Замкнутость: Результатом сложения любых двух точек на кривой также является точка на этой же кривой.
- Ассоциативность: Для любых трех точек P, Q, R на кривой верно: (P+Q)+R=P+(Q+R).
- Существование нейтрального элемента: Нейтральным элементом группы точек на кривой является точка в бесконечности O, также называемая точкой на кривой в бесконечности. Для любой точки P на кривой верно: P+O=O+P=P.
- Существование обратного элемента: Для каждой точки P на кривой существует точка Q, такая что P+Q=O, где O - нейтральный элемент.
В контексте эллиптической криптографии часто используются две формы записи операций: аддитивная и мультипликативная:
- Аддитивная запись: Операция сложения двух точек на кривой обозначается символом "+". Например, P+Q означает сумму точек P и Q.
- Мультипликативная запись: Вместо сложения точек используется умножение точки на скаляр (целое число). Например, n⋅P означает сумму точки P с самой собой n раз.
Мультипликативная запись обычно используется в криптографических алгоритмах, таких как генерация ключей и подписи, поскольку позволяет эффективно работать с большими числами.
- Порядок точки: Порядок точки P на эллиптической кривой - это количество точек n, которые можно получить, складывая P с самим собой несколько раз, пока не получится точка в бесконечности O. Формально, порядок точки P обозначается как #P.
- Циклическая группа: Множество всех точек на кривой, порожденное одной точкой G, и всех их сумм, образует циклическую группу. Это означает, что существует некоторое целое число n, такое что nG=O, и для каждого целого числа m существует точка P, такая что P=mG. Эта особенность имеет фундаментальное значение в криптографии, так как позволяет строить протоколы, основанные на сложности нахождения дискретного логарифма в циклической группе.
Python: Скопировать в буфер обмена
Эллиптическая криптография (ЭК) представляет собой криптографические методы, основанные на математических свойствах эллиптических кривых. Она обладает несколькими преимуществами по сравнению с классическими методами, такими как RSA:
- Бóльшая безопасность при том же размере ключа: ЭК обеспечивает такой же уровень безопасности при использовании ключей меньшей длины по сравнению с классическими криптосистемами. Например, 256-битный ключ в ЭК обеспечивает уровень безопасности, сравнимый с 3072-битным ключом RSA.
- Эффективность использования ресурсов: При работе с большими числами, характерными для криптографических операций, ЭК обеспечивает более эффективное использование ресурсов процессора и памяти.
- Более высокая стойкость к квантовым атакам: ЭК считается более стойкой к квантовым атакам по сравнению с классическими криптосистемами. Это связано с тем, что алгоритмы квантовых компьютеров не могут решать задачу дискретного логарифмирования на эллиптических кривых существенно быстрее, чем классические компьютеры.
Шифрование с использованием эллиптических кривых основано на операции умножения точки на скаляр (целое число). Пусть P - это точка на эллиптической кривой, n - это целое число (ключ). Шифрование выполняется путем умножения точки P на ключ n, что дает точку Q=n⋅P. Для дешифрования используется обратная операция - умножение точки Q на обратное значение ключа.
Пример шифрования и дешифрования на основе эллиптических кривых на Python:
Python: Скопировать в буфер обмена
Получаем вывод:

3. Эллиптические кривые в цифровых подписях
Эллиптические кривые также активно используются для создания и проверки цифровых подписей. Протокол подписи, такой как ECDSA (Elliptic Curve Digital Signature Algorithm), использует математические операции на эллиптических кривых для создания цифровой подписи и проверки её подлинности.
Пример создания и проверки цифровой подписи на основе эллиптических кривых на Python:
Python: Скопировать в буфер обмена
Получаем вывод:
4. Протоколы обмена ключами на основе эллиптических кривых (ECDH)
Протоколы обмена ключами на основе эллиптических кривых, такие как ECDH (Elliptic Curve Diffie-Hellman), позволяют двум сторонам безопасно обмениваться секретным ключом, который затем может использоваться для шифрования и дешифрования сообщений.
Пример реализации протокола ECDH на Python:
Python: Скопировать в буфер обмена
Получаем вывод:

Проблема дискретного логарифмирования (DLP) на эллиптических кривых является фундаментальной задачей в криптографии, которая заключается в нахождении целого числа k из уравнения P=k⋅G, где P - заданная точка на кривой, G - точка порождающая циклическую группу, k - целое число (ключ).
Сложность решения проблемы DLP на эллиптических кривых базируется на отсутствии эффективного алгоритма, который мог бы решить её за разумное время, особенно при использовании больших ключей. Лучшие известные алгоритмы для атак на проблему DLP на эллиптических кривых в настоящее время базируются на общих методах решения дискретного логарифма. Однако, из-за сложности эллиптических кривых и специально выбранных параметров, даже лучшие известные алгоритмы требуют экспоненциального времени для решения задачи DLP при достаточно больших ключах.
2. Размер ключа и сложность атак
Размер ключа в криптографии на эллиптических кривых играет критическую роль в обеспечении безопасности криптосистемы. Длина ключа определяется величиной параметра n, который является порядком группы точек на кривой. Сложность атак на криптосистему с использованием эллиптических кривых напрямую зависит от размера ключа, который, в свою очередь, определяется длиной параметра n.
Общепринятой практикой является использование ключей длиной от 128 до 256 бит в криптографических протоколах на основе эллиптических кривых. Для достижения соответствующего уровня безопасности рекомендуется выбирать ключи с длиной, обеспечивающей устойчивость к известным атакам на проблему DLP.
3. Стандарты и рекомендации по выбору параметров
Стандарты и рекомендации по выбору параметров для криптографии на эллиптических кривых разрабатываются и поддерживаются различными организациями, такими как NIST (National Institute of Standards and Technology), SECG (Standards for Efficient Cryptography Group) и ANSI (American National Standards Institute). Эти стандарты включают в себя рекомендации по выбору кривых, параметров кривых, а также методы проверки и подтверждения безопасности эллиптических кривых.
Одним из примеров стандартов является стандарт NIST FIPS 186-4, который определяет требования к использованию эллиптических кривых в криптографии. Стандарт рекомендует использовать определенные наборы параметров, такие как кривые NIST P-256 и NIST P-384, и предоставляет руководство по проверке безопасности кривых.
- Квантово-стойкие кривые: Исследователи работают над разработкой эллиптических кривых и алгоритмов, которые будут устойчивы к атакам квантовыми компьютерами. Это может включать в себя создание кривых с большими параметрами или использование альтернативных математических структур.
- Протоколы квантового ключа: Эллиптические кривые могут использоваться в протоколах квантового ключа для безопасного обмена ключами и создания защищенных каналов связи. Квантовые компьютеры могут значительно повлиять на эффективность этих протоколов, исключив возможность взлома на основе квантовых атак.
Специально для ~/XSS.IS
Всех любителей, а также ненавистников математики рад видеть тут =)
ВВЕДЕНИЕ В ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ
1. Определение эллиптических кривыхВВЕДЕНИЕ В ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ
Эллиптическая кривая представляет собой геометрическую структуру, определяемую уравнением вида:
(★),
2. Математические основы- Уравнение кривой: Уравнение (★) определяет форму эллиптической кривой. Коэффициенты a и b влияют на ее кривизну и форму.
- Операции над точками: Операции над точками на эллиптической кривой включают в себя сложение точек и удвоение точек. Сложение точек определяется геометрически и связано с поиском пересечения кривой с прямой, проходящей через две заданные точки. Удвоение точки также является геометрической операцией, представляющей собой поиск касательной к кривой в заданной точке и нахождение её второго пересечения с кривой.
3. Зачем они используются в криптографииЭллиптические кривые нашли широкое применение в криптографии благодаря своим уникальным математическим свойствам, которые делают их особенно подходящими для различных криптографических задач. Основные преимущества использования эллиптических кривых включают в себя:
- Безопасность: Эллиптические кривые обеспечивают высокий уровень безопасности при использовании в криптографических протоколах. Это связано с тем, что проблема дискретного логарифмирования на эллиптических кривых сложнее для решения по сравнению с аналогичными задачами для других математических структур.
- Эффективность: В сравнении с классическими методами криптографии, такими как RSA, использование эллиптических кривых позволяет достигать того же уровня безопасности при меньших объемах ключей и операций.
- Масштабируемость: Эллиптические кривые позволяют строить криптографические протоколы, способные работать с небольшими вычислительными ресурсами.
ОСНОВНЫЕ ПОНЯТИЯ
1. Группы точек на эллиптической кривойГруппой точек на эллиптической кривой называется множество всех точек кривой вместе с определенной операцией, обычно называемой сложением точек. Формально, пусть E - эллиптическая кривая, а P и Q - две её точки. Операция сложения P+Q определяется геометрически и зависит от конкретного вида кривой. Основные свойства группы точек на эллиптической кривой включают:
- Замкнутость: Результатом сложения любых двух точек на кривой также является точка на этой же кривой.
- Ассоциативность: Для любых трех точек P, Q, R на кривой верно: (P+Q)+R=P+(Q+R).
- Существование нейтрального элемента: Нейтральным элементом группы точек на кривой является точка в бесконечности O, также называемая точкой на кривой в бесконечности. Для любой точки P на кривой верно: P+O=O+P=P.
- Существование обратного элемента: Для каждой точки P на кривой существует точка Q, такая что P+Q=O, где O - нейтральный элемент.
2. Аддитивная и мультипликативная запись операцийВ контексте эллиптической криптографии часто используются две формы записи операций: аддитивная и мультипликативная:
- Аддитивная запись: Операция сложения двух точек на кривой обозначается символом "+". Например, P+Q означает сумму точек P и Q.
- Мультипликативная запись: Вместо сложения точек используется умножение точки на скаляр (целое число). Например, n⋅P означает сумму точки P с самой собой n раз.
Мультипликативная запись обычно используется в криптографических алгоритмах, таких как генерация ключей и подписи, поскольку позволяет эффективно работать с большими числами.
3. Порядок точек и циклическая группа- Порядок точки: Порядок точки P на эллиптической кривой - это количество точек n, которые можно получить, складывая P с самим собой несколько раз, пока не получится точка в бесконечности O. Формально, порядок точки P обозначается как #P.
- Циклическая группа: Множество всех точек на кривой, порожденное одной точкой G, и всех их сумм, образует циклическую группу. Это означает, что существует некоторое целое число n, такое что nG=O, и для каждого целого числа m существует точка P, такая что P=mG. Эта особенность имеет фундаментальное значение в криптографии, так как позволяет строить протоколы, основанные на сложности нахождения дискретного логарифма в циклической группе.
Пример кода на Python для сложения точек на эллиптической кривой (предполагается, что кривая задана уравнением (★) и операция сложения точек определена):Python: Скопировать в буфер обмена
Код:
def add_points(P, Q, a, b):
# Проверка на специальные случаи: если одна из точек - бесконечность, возвращаем другую точку
if P == 'O':
return Q
if Q == 'O':
return P
x1, y1 = P
x2, y2 = Q
# Рассчитываем наклон прямой, проходящей через точки P и Q
if P != Q:
slope = (y2 - y1) / (x2 - x1)
else:
# Если P и Q совпадают, используем формулу для касательной
slope = (3 * x1 ** 2 + a) / (2 * y1)
# Вычисляем координаты новой точки
x3 = slope ** 2 - x1 - x2
y3 = slope * (x1 - x3) - y1
# Возвращаем результат в формате кортежа
return (x3, y3)
def main():
# Пример использования функции
P = (2, 5)
Q = (-1, -1)
a = 5
b = 7
result = add_points(P, Q, a, b)
print("Результат сложения точек P и Q:", result)
if __name__ == "__main__":
main()ПРИМЕНЕНИЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ В КРИПТОГРАФИИ
1. Эллиптическая криптография, преимущества перед классическими методамиЭллиптическая криптография (ЭК) представляет собой криптографические методы, основанные на математических свойствах эллиптических кривых. Она обладает несколькими преимуществами по сравнению с классическими методами, такими как RSA:
- Бóльшая безопасность при том же размере ключа: ЭК обеспечивает такой же уровень безопасности при использовании ключей меньшей длины по сравнению с классическими криптосистемами. Например, 256-битный ключ в ЭК обеспечивает уровень безопасности, сравнимый с 3072-битным ключом RSA.
- Эффективность использования ресурсов: При работе с большими числами, характерными для криптографических операций, ЭК обеспечивает более эффективное использование ресурсов процессора и памяти.
- Более высокая стойкость к квантовым атакам: ЭК считается более стойкой к квантовым атакам по сравнению с классическими криптосистемами. Это связано с тем, что алгоритмы квантовых компьютеров не могут решать задачу дискретного логарифмирования на эллиптических кривых существенно быстрее, чем классические компьютеры.
2. Шифрование и дешифрование с использованием эллиптических кривыхШифрование с использованием эллиптических кривых основано на операции умножения точки на скаляр (целое число). Пусть P - это точка на эллиптической кривой, n - это целое число (ключ). Шифрование выполняется путем умножения точки P на ключ n, что дает точку Q=n⋅P. Для дешифрования используется обратная операция - умножение точки Q на обратное значение ключа.
Пример шифрования и дешифрования на основе эллиптических кривых на Python:
Python: Скопировать в буфер обмена
Код:
import ecdsa
from ecdsa.util import string_to_number, number_to_string
# Генерация ключей
def generate_keypair():
sk = ecdsa.SigningKey.generate(curve=ecdsa.SECP256k1)
vk = sk.get_verifying_key()
return sk, vk
# Шифрование
def encrypt(message, public_key):
point = public_key.pubkey.point
key = ecdsa.util.randrange(ecdsa.SECP256k1.order)
cipher_point = key * point
return (cipher_point, key)
# Дешифрование
def decrypt(ciphertext, private_key):
cipher_point, key = ciphertext
shared_point = key * cipher_point
shared_key = string_to_number(shared_point.x().to_bytes(32, 'big'))
return shared_key
# Пример использования
if __name__ == "__main__":
# Генерация ключей
private_key, public_key = generate_keypair()
# Шифрование сообщения
message = b"Hello, XSS!"
ciphertext, key = encrypt(message, public_key)
print("Зашифрованное сообщение (точка шифрации):", ciphertext)
print("Ключ, использованный для шифрования:", key)
# Дешифрование сообщения
decrypted_key = decrypt((ciphertext, key), private_key)
print("Расшифрованный ключ:", decrypted_key)Получаем вывод:
3. Эллиптические кривые в цифровых подписях
Эллиптические кривые также активно используются для создания и проверки цифровых подписей. Протокол подписи, такой как ECDSA (Elliptic Curve Digital Signature Algorithm), использует математические операции на эллиптических кривых для создания цифровой подписи и проверки её подлинности.
Пример создания и проверки цифровой подписи на основе эллиптических кривых на Python:
Python: Скопировать в буфер обмена
Код:
from ecdsa import SigningKey, VerifyingKey
# Генерируем закрытый и открытый ключи
private_key = SigningKey.generate() # Генерация закрытого ключа
public_key = private_key.get_verifying_key() # Получение открытого ключа
# Шифрование (подпись)
message = b"Hello, XSS!"
signature = private_key.sign(message)
# Дешифрование (проверка подписи)
try:
public_key.verify(signature, message)
print("Подпись верна.")
except ecdsa.BadSignatureError:
print("Ошибка: неверная подпись.")Получаем вывод:
Протоколы обмена ключами на основе эллиптических кривых, такие как ECDH (Elliptic Curve Diffie-Hellman), позволяют двум сторонам безопасно обмениваться секретным ключом, который затем может использоваться для шифрования и дешифрования сообщений.
Пример реализации протокола ECDH на Python:
Python: Скопировать в буфер обмена
Код:
from ecdsa import ECDH, SigningKey, VerifyingKey, SECP256k1
# Генерация закрытого и открытого ключей для Alice
alice_sk = SigningKey.generate(curve=SECP256k1)
alice_vk = alice_sk.get_verifying_key()
# Генерация закрытого и открытого ключей для Bob
bob_sk = SigningKey.generate(curve=SECP256k1)
bob_vk = bob_sk.get_verifying_key()
# Обмен открытыми ключами
alice_ecdh = ECDH(curve=SECP256k1)
alice_ecdh.generate_private_key()
alice_shared_key = alice_ecdh.get_public_key()
bob_ecdh = ECDH(curve=SECP256k1)
bob_ecdh.generate_private_key()
bob_shared_key = bob_ecdh.get_public_key()
# Установка общих открытых ключей
alice_ecdh.load_received_public_key(bob_shared_key)
bob_ecdh.load_received_public_key(alice_shared_key)
# Вычисление общего секретного ключа на стороне Alice
alice_secret = alice_ecdh.generate_sharedsecret_bytes()
# Вычисление общего секретного ключа на стороне Bob
bob_secret = bob_ecdh.generate_sharedsecret_bytes()
# Проверка совпадения общих секретных ключей
if alice_secret == bob_secret:
print("Секретные ключи совпадают.")
else:
print("Секретные ключи не совпадают.")Получаем вывод:
БЕЗОПАСНОСТЬ И ПРОБЛЕМЫ
1. Проблема дискретного логарифмирования на эллиптических кривыхПроблема дискретного логарифмирования (DLP) на эллиптических кривых является фундаментальной задачей в криптографии, которая заключается в нахождении целого числа k из уравнения P=k⋅G, где P - заданная точка на кривой, G - точка порождающая циклическую группу, k - целое число (ключ).
Сложность решения проблемы DLP на эллиптических кривых базируется на отсутствии эффективного алгоритма, который мог бы решить её за разумное время, особенно при использовании больших ключей. Лучшие известные алгоритмы для атак на проблему DLP на эллиптических кривых в настоящее время базируются на общих методах решения дискретного логарифма. Однако, из-за сложности эллиптических кривых и специально выбранных параметров, даже лучшие известные алгоритмы требуют экспоненциального времени для решения задачи DLP при достаточно больших ключах.
2. Размер ключа и сложность атак
Размер ключа в криптографии на эллиптических кривых играет критическую роль в обеспечении безопасности криптосистемы. Длина ключа определяется величиной параметра n, который является порядком группы точек на кривой. Сложность атак на криптосистему с использованием эллиптических кривых напрямую зависит от размера ключа, который, в свою очередь, определяется длиной параметра n.
Общепринятой практикой является использование ключей длиной от 128 до 256 бит в криптографических протоколах на основе эллиптических кривых. Для достижения соответствующего уровня безопасности рекомендуется выбирать ключи с длиной, обеспечивающей устойчивость к известным атакам на проблему DLP.
3. Стандарты и рекомендации по выбору параметров
Стандарты и рекомендации по выбору параметров для криптографии на эллиптических кривых разрабатываются и поддерживаются различными организациями, такими как NIST (National Institute of Standards and Technology), SECG (Standards for Efficient Cryptography Group) и ANSI (American National Standards Institute). Эти стандарты включают в себя рекомендации по выбору кривых, параметров кривых, а также методы проверки и подтверждения безопасности эллиптических кривых.
Одним из примеров стандартов является стандарт NIST FIPS 186-4, который определяет требования к использованию эллиптических кривых в криптографии. Стандарт рекомендует использовать определенные наборы параметров, такие как кривые NIST P-256 и NIST P-384, и предоставляет руководство по проверке безопасности кривых.
БУДУЩЕЕ
В будущем эллиптические кривые могут сыграть важную роль в развитии квантовой криптографии:- Квантово-стойкие кривые: Исследователи работают над разработкой эллиптических кривых и алгоритмов, которые будут устойчивы к атакам квантовыми компьютерами. Это может включать в себя создание кривых с большими параметрами или использование альтернативных математических структур.
- Протоколы квантового ключа: Эллиптические кривые могут использоваться в протоколах квантового ключа для безопасного обмена ключами и создания защищенных каналов связи. Квантовые компьютеры могут значительно повлиять на эффективность этих протоколов, исключив возможность взлома на основе квантовых атак.
ЗАКЛЮЧЕНИЕ
В данной статье мы затронули очень важное понятие в рамках криптографии. Всех заинтересовавшихся благодарю за внимание. Надеюсь многим понравилось и объяснение материала не показалось слишком сложным и душным. В любом случае буду рад увидеть Ваши комментарии касаемо данной статьи. Еще увидимся!